Neste artigo apresentaremos um dos critérios de seleção de correia transportadora, os tipos de tensões atuantes no transportador para especificar e selecionar uma correia transportadora.
Este artigo foi desenvolvido por Willian de Castro Toledo
INTRODUÇÃO
Calcular e saber as tensões atuantes é o ponto de partida para especificar a potência requerida do acionamento, capacidade de carga da correia transportadora e dimensionamento dos demais componentes do transportador, além de estabelecer os limites de operação do sistema.
Nota-se que neste artigo, onde é citado “tensão” também pode ser entendido como “força”.
A principal tensão neste contexto, é a tensão efetiva ou também chamada de força periférica (Te), que é a força tangencial requerida no tambor motriz para movimentar a carga de material que esta sendo manuseado pela correia transportadora. Para que este movimento aconteça, o acionamento deverá ter força suficiente para superar as forças de atrito presentes nos elementos do transportador, peso do material transportado e elevações de acordo com o perfil do transportador.
Basicamente atrito é definido como uma força que se opõe ao movimento dos corpos. Em resumo, a tensão efetiva (Te) é a força necessária no tambor motriz para vencer a soma algébrica de todas as resistências (atritos) ao movimento da correia transportadora, ou seja, tensão efetiva > atrito.
A capacidade do motor de acionamento em transmitir a tensão efetiva (Te) para a correia transportadora através do tambor motriz é governada pelo seguinte conjugado de grandezas:
- Coeficiente de atrito entre a correia e o tambor motriz;
- Ângulo de abraçamento entre a correia e o tambor motriz;
- Diferença das forças na correia entre os dois lados do tambor (T1 e T2);
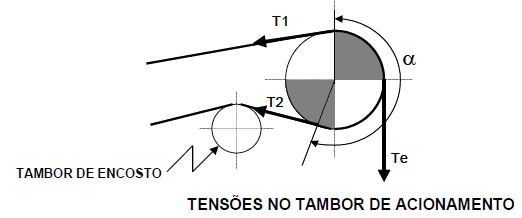
A figura 01 mostra o esquema das tensões atuantes no tambor motriz (Te, T1 e T2).
TENSÃO EFETIVA (TE)
Como já mencionado acima, a tensão efetiva (Te) é a força tangencial necessária no tambor motriz para superar as forças de atrito e permitir o movimento da correia transportadora. Neste artigo será demonstrado o cálculo da tensão efetiva (Te) através do método CEMA DE CONCEPÇÃO UNIVERSAL, que atualmente é o método mais aceito pelos projetistas devido seu escopo ser mais abrangentes em referência aos outros métodos.
De acordo com a CEMA, o método universal para determinar a tensão efetiva (Te) da correia transportadora pode ser aplicado a:
- Um transportador de comprimento qualquer;
- Pontos de carregamento de fluxo simples ou múltiplos;
- Combinações de trechos inclinados, em declinio e/ou horizontais com curvas verticais ou horizontais;
- Correia com carcaça de lona ou cabo de aço;
- Qualquer perfil de transportador;
- Unidirecional ou reversivel;
- Acionamento simple ou múltiplo;
- Esticamento fixo ou automático;
Este método se limita ao estado estático ou estado de operação em velocidade constante do transportador. No entanto, ele também pode ser utilizado para prever a alteração de atrito uma vez que a velocidade da correia se altera de maneira uniforme durante a partida ou parada, e tem como objetivo representar de melhor forma as particularidades encontradas em cada parte do equipamento e possibilitar o cálculo mais preciso de qualquer transportador, neste caso, o transportador é dividido em trechos.
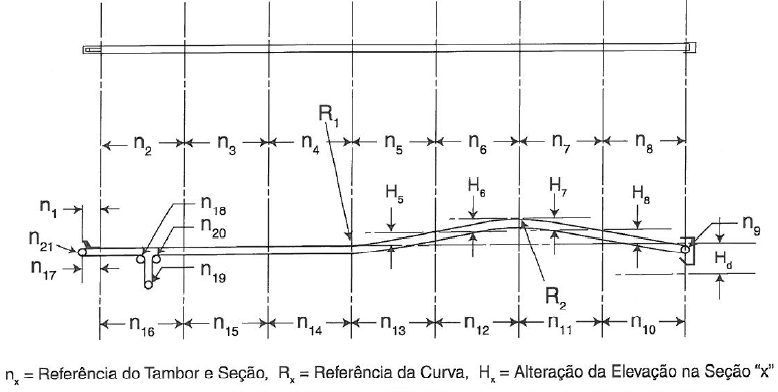
A cada trecho “n” são avaliadas as resistências locais ao movimento da correia sendo estas acrescidas como tensão de correia (força necessária para vencer o atrito). A figura 02 mostra um exemplo de perfil de transportador dividido por seções tanto para o lado de carga quanto para o lado de retorno da correia transportadora.
Desta forma, a tensão no final de qualquer trecho será dada pela soma da tensão no final do trecho anterior com as resistências calculadas para o trecho em questão. O acréscimo total de tensão de correia ΔTn é dado pela equação a seguir:

Ressalta-se que neste artigo não será mostrado como se calcula cada variável deste método, sendo que as equações e seu detalhamento podem ser encontradas diretamente no manual da CEMA, porém, cada componente que oferece resistência ao movimento e que demanda de acréscimo de tensão na correia será explicado a seguir.
Tensões relacionadas à energia – ∑ΔT Energy
∑ΔT Energy = ΔTHn + ΔTamn
ΔTHn = Alteração na tensão da correia para elevar ou abaixar o material e a correia
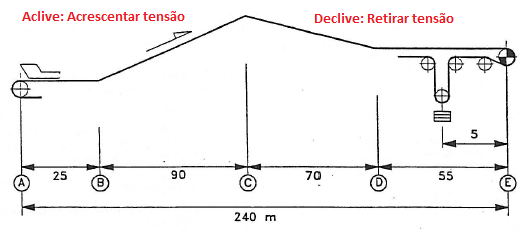
Esta força está relacionada exclusivamente aos desníveis encontrados no perfil do transportador, podendo ser positiva (aclive), negativa (declive) ou nula. Por exemplo, se o perfil do transportador em determinado trecho possui um aclive, vai haver um aumento de tensão, se houver um declive resulta em redução de tensão, uma vez que a gravidade tende a manter a correia para baixo.
ΔTamn = Acréscimo de tensão de correia para acelerar continuamente o material até a velocidade de transporte
Deve-se fornecer energia cinética ao material a granel para acelera-lo de modo a coincidir com a velocidade da correia. Esta força de aceleração é fornecida pela correia por meio de um aumento de tensão no (os) ponto (s) de carregamento na direção do movimento da correia. Será pouco significante em transportadores de grande porte e pequena capacidade e bastante expressiva em transportadores curtos e de grande capacidade. É uma componente de força fortemente influenciada pelo chute de transferência, sendo possível minimizá-la com a utilização de um chute bem projetado para este fim.
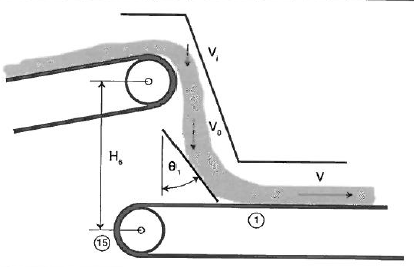
Principais resistências – ∑ΔMain
∑ΔMain = ΔTssn + ΔTisn + ΔTiWn + ΔTbin + ΔTimn + ΔTsn + ΔTmzn
ΔTssn = Acréscimo de tensão devido ao deslizamento da correia na vedação da guia de material
Esta força está relacionada à pressão de contato entre vedação da guia de material e a correia, só é expressiva em relação à força total em transportadores de pequeno porte e capacidade.
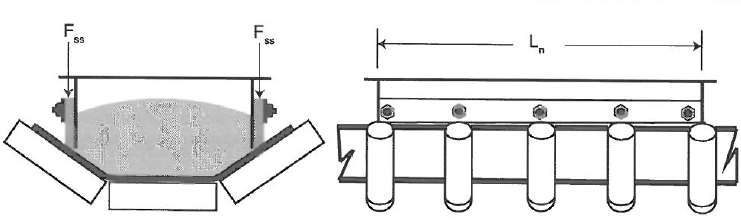
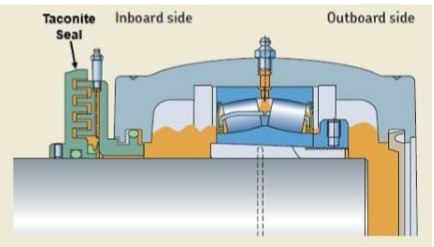
ΔTisn = Acréscimo de tensão de correia devido ao atrito das vedações dos rolos
Os rolos resistem aos movimentos de rotação e da correia por meio de mecanismos internos ao rolo. Esta força está relacionada ao tipo de vedação utilizada para evitar contaminação por agentes externos aos rolamentos dos rolos, bem como com a graxa utilizada. Devido a quantidade de rolos instalados, esta força é bem expressiva em transportadores longos.
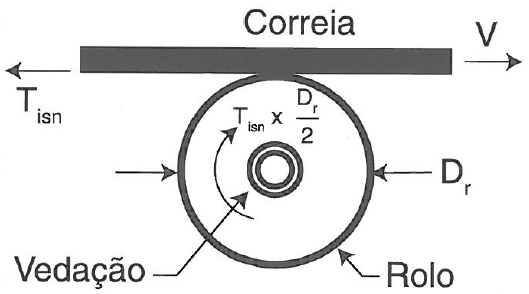
ΔTiWn = Acréscimo de tensão de correia devido ao atrito dos rolos causados pela carga transportada
Esta componente de força tem relação com a carga de material sobre os roletes. Quanto maior a carga, maior será o atrito. Estas perdas por atrito, variam de acordo com o material e o peso da correia carregada pelo roletes e, para algumas, de acordo com a tensão da correia.
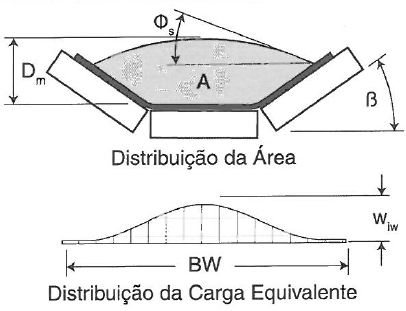
ΔTbin = Acréscimo de tensão de correia devido à deformação visco-elástica da correia
Esta força é causada pela deformação que a correia sofre ao passar pelos rolos. Quando ocorre a passagem da correia pelos rolos, a cobertura inferior da correia é comprimida e sofre uma pequena deformação, também chamada de indentação, resultando em um esforço resistente ao movimento da correia. Assim que a correia deixa os rolos, força de compressão deixa de agir e a deformação é restaurada, resultando em um esforço positivo para o movimento da correia. Este atrito é um fator importante para transportadores longos, para transportadores curtos, não há perdas significantes para adicionar na tensão total da correia.

O uso de coberturas de correia do tipo LRR (Low Rolling Resistance) traduzindo para o português significa composto com baixa resistência ao rolamento pode ajudar a reduzir este atrito por identação.
ΔTimn = Acréscimo de tensão de correia devido ao desalinhamento dos roletes
Roletes desalinhados introduzem uma componente de força devido ao atrito que estes terão com a correia retardando o seu movimento. A intensidade desta força está relacionada com o grau de desalinhamento e a carga atuante sobre os rolos. É possível minimizá-la, bem como reduzir o desgaste dos rolos e cobertura da correia através de uma montagem criteriosa do transportador.
Ressalta-se que a tentativa de alinhar a correia inclinando os rolos de carga em 2 graus, pode aumentar consideravelmente o atrito com a correia transportadora, necessitando assim acréscimo de tensão, portanto a aplicação deste recurso deve ser bem avaliado.
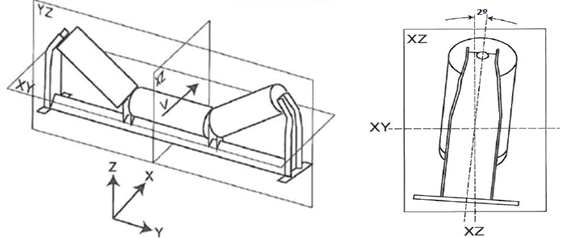
ΔTsn = Acréscimo de tensão de correia devido ao atrito do material com as guias de material
É a força necessária para superar o atrito do material manuseado com a guia lateral na região de carregamento do transportador, e é geralmente maior por unidade de comprimento da guia lateral do que a força para mover a correia carregada sobre os roletes. Quando o comprimento total do transportador for muito maior do que o comprimento das guias laterais, os requisitos de tensão nas guias são relativamente baixos, ou seja, este atrito é mais critico para transportadores curtos, contudo, se uma grande parte do transportador estiver guias laterais instaladas, o acréscimo de tensão poderá ser um fator importante, como por exemplo, correia que recebe alimentação de vários silos e possuem vários chutes com guias laterais.
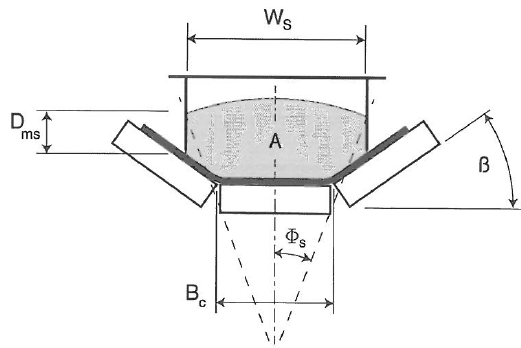
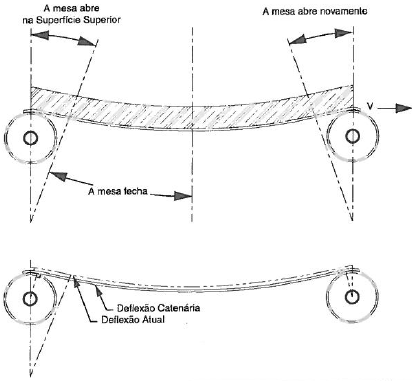
ΔTmzn = Acréscimo de tensão de correia devido ao movimento do material transportado entre roletes
Devido ao peso da correia e do material, a correia forma um arco, ou flecha entre os roletes adjacentes também chamado de “SAG”. Normalmente, esta flecha é limitada a 2% entre os centros dos roletes, mas pode variar. A flecha causa uma deformação do material e aumenta a resistência ao movimento da correia, com isto, é necessário um acréscimo de força para movimentação da correia.
Fontes de pontos de tensão – ∑ΔPoint
∑ΔPoint = ΔTpxn + ΔTprn + ΔTbcn
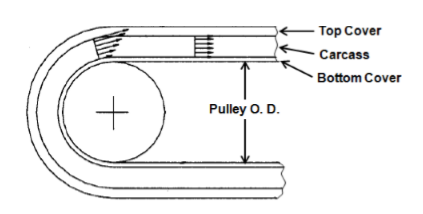
ΔTpxn = Acréscimo de tensão devido a passagem na correia nos tambores
Esta força está relacionada com a rigidez da correia ao passar nos tambores. A resistência da correia à flexão sob os tambores é em função do diâmetro do tambor e da sua rigidez, que por sua vez depende da temperatura ambiente e construção da carcaça.
ΔTprn = Acréscimo de tensão de correia devido ao atrito dos rolamentos dos tambores
A resistência do tambor para girar é em função do atrito no mancal de rolamento, do lubrificante e do atrito da vedação. O atrito no mancal de rolamento depende da carga sobre os mancais e do lubrificante utilizado, enquanto os atritos da vedação são, geralmente independentes da carga.
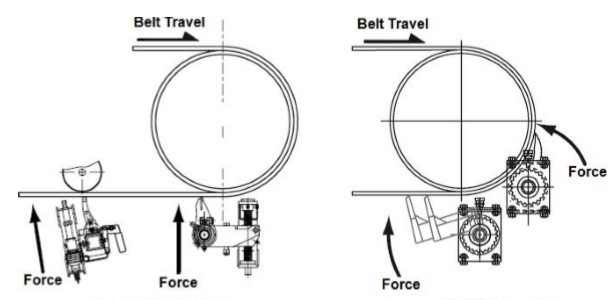
ΔTbcn = Acréscimo de tensão de correia devido aos raspadores de limpadores de correia
Para remover os materiais remanescentes é necessário que os raspadores e limpadores exerçam certa pressão sobre a correia, causando um acréscimo de força para sua movimentação. Quanto mais estes dispositivos são instalados, maior será o acréscimo de tensão.
Para finalizar sobre as principais resistências no transportador, uma amostragem realizada por Hager e Hintz (1993) identifica que 61% das resistências presentes no transportador é referente a deformação visco-elástica da correia também conhecida como indentação da correia transportadora com os rolos e em seguida com 18% a resistência provocada pela flexão do material manuseado sobre a correia.

LIMITAÇÕES DO MÉTODO CEMA CONCEPÇÃO UNIVERSAL E ANÁLISE DINÂMICA
O método CEMA concepção universal se limita ao estado estático ou em regime considerando o transportador operando com velocidade e carregamento constante, o que não traduz a realidade operacional destes equipamentos. Neste caso, para transportadores que apresentam as caracterisitcas abaixo, o cálculo da tensão efetiva (Te) pelo método de análise dinâmica é recomendado.
- Acionamentos múltiplos;
- Grandes elevações, principalmente quando o sistema de esticamento se encontra próximo ao(s) acionamento(s);
- Curvas horizontais;
- Média a alta capacidade de regeneração com freios de alto torque;
- Capacidades de transporte acima de 7.250 t/h;
- Velocidades de transporte acima de 5,0 m/s.
A análise dinâmica apresenta cálculos realizados por meio de softwares que utilizam um complexo modelo matemático e podem simular de forma realista os regimes transientes do transportador, principalmente os regimes mais criticos como a partida e parada da correia.
TENSÃO NO RETORNO (T2)
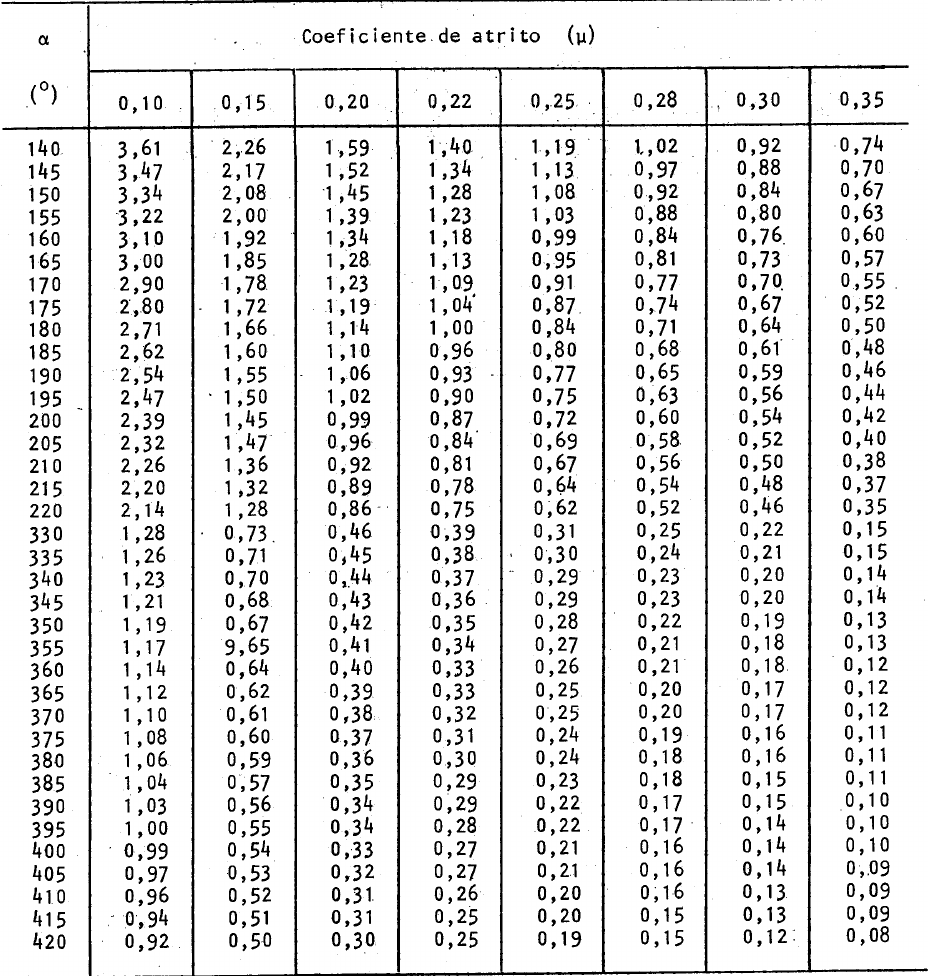
Também conhecida como tensão no lado “bambo”, a T2 é a força minima para manter o esticamento da correia e não permitir o seu deslizamento no tambor de acionamento. Desta forma, para que a tensão efetiva (Te) seja confiavelmente transmitida de modo a prover o movimento da correia, é necessário fixar o valor de menor força T2 na saída do tambor de acionamento dado uma condição de atrito e abraçamento entre a correia e o tambor motriz. O valor de T2 pode ser calculado pela equação:

Te = Tensão efetiva
e = base do logaritmo neperiano = 2,718
µ = coeficiente de atrito entre a superfície do tambor de acionamento e a cobertura da correia
ɸ = ângulo de abraçamento da correia no tambor de acionamento

TENSÃO MÁXIMA (T1)
A tensão máxima (T1) se refere à máxima força à qual a correia será submetida na entrada do tambor de acionamento durante sua operação e é o valor determinante para especificar uma correia transportadora, ou seja, a correia deverá ser selecionada com resistência suficiente de acordo com o valor encontrado de T1
O cálculo da T1 é feito através do equibilibrio das forças no tambor motriz pela equação:
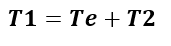
CONCLUSÃO
Foi mostrado neste artigo as principais tensões atuantes na correia transportadora, com destaque para a tensão efetiva, que é a força necessária para superar os atritos presentes no transportador e possibilitar o movimento da correia transportadora através do método CEMA de concepção universal.
É importante os profissionais da manutenção e operação conhecerem as principais resistências operacionais presentes no transportador de modo a indentificar possiveis fontes de aumento de potência requerida no acionamento, que por consequência provoca desarmes e/ou aumento no consumo de energia elétrica.
Por fim, foi mostrado a T2 que é a força minima na saída do tambor motriz para manter o esticamento da correia e evitar possiveis deslizamentos entre a correia e o tambor motriz e a T1 que a força máxima na entrada deste tambor, sendo esta a força determinante para especificar uma correia transportadora.
REFERÊNCIAS
ASSOCIAÇÃO BRASILEIRA DE NORMAS TÉCNICAS (ABNT). NBR-8205. Transportadores contínuos – Transportadores de correia – Cálculo de força e potência. Rio de Janeiro. 2014.
Conveyor Equipment Manufacturers Association – CEMA. Belt Conveyors for Bulk Materials. 7º Edição, 1º Edição em Português. ABNT, 2014.
HAGER, M.; HINTZ. A. “The Energy-Saving Design of Belts for Long Conveyor Systems. Bulk Solids Handling. v.13, n.4, p.749-758, 1993.