Este artigo foi desenvolvido por Caio Bertholdi
1 – INTRODUÇÃO
O cálculo da inércia do transportador de correia se faz necessário para determinar os tempos de parada e partida do equipamento. Em uma linha de rota de correias, tal cálculo é de suma importância para garantir que o tempo de parada natural da correia alimentadora não seja maior que o da correia receptora.
Caso isso aconteça, poderá haver falhas operacionais graves como o entupimento do chute de transferência, impossibilitando a correia receptora de partir devido ao peso do material acumulado no chute. Para estes casos, deve-se utilizar volantes de inércia a fim de aumentar o tempo de parada da correia receptora.
Ao realizar os cálculos de parada e partida utilizando a análise estática, considera-se que todas as massas são aceleradas ao mesmo tempo, admitindo que a correia é um corpo rígido e as massas rotativas e a correia estão rigidamente conectadas. Na realidade, o torque produzido no motor e transmitido para a correia por meio do tambor de acionamento, cria uma onda de tensão que inicia o movimento da correia gradualmente à medida que se propaga ao longo da correia.
Para correia não muito longas, a aproximação para o modelo estático já é suficiente. Portanto, para a nossa análise de inércia será adotado o modelo estático.
2 – TEMPO DE PARTIDA DA CORREIA
Antes de entender o comportamento da correia na parada, iremos entender como ocorre a partida da mesma.
Supondo que a correia seja o bloco branco demonstrado na figura abaixo, o somatório de todas as forças peso e de atrito, que impedem a mesma de entrar em movimento é denominado Tensão Efetiva (Te). O método para se determinar Te está contido na CEMA 7th e por envolver um número muito grande de variáveis, não é o objetivo do artigo em questão.
Para mover o bloco, necessitaremos de uma força F maior que Te, sendo que quanto maior a força F, menor será o tempo para que o bloco atinja uma velocidade final desejada. Como o bloco está parado, Vo=0.
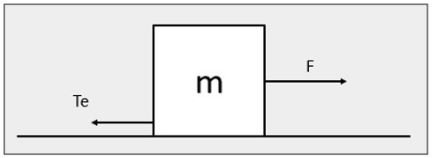
Aplicando a segunda lei de Newton para este estudo de caso, teremos:
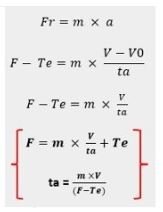
Onde:
F= Força gerada pelo torque dos acionamentos para partir a correia (N)
Te= Tensão efetiva da correia (N)
m = Massa total movida pelo transportador (Kg). É a soma de todo o peso do material transportado ao longo da correia, do peso equivalente das partes rotativas (motores, redutores, acoplamentos e tambores motrizes) e do peso equivalente dos equipamentos móveis do transportador (material, tambores movidos, correia e rolos).
ta = tempo de aceleração da correia (s)
V= Velocidade nominal da correia (m/s)
3 – TEMPO DE PARADA DA CORREIA
Após atingir a velocidade constante, pelas leis de Newton, o somatório das forças atuantes na correia é nulo, sendo assim, a força dos motores para mover a correia será igual a Tensão Efetiva (Te).

Quando ocorre o desligamento dos motores, a força que irá desacelerar a correia será Te, a uma velocidade Vo igual a velocidade da correia e até atingir o repouso (V=0).

Aplicando a segunda lei de Newton para este estudo de caso, teremos:

Onde:
Te= Tensão efetiva da correia (N)
m = Massa total movida pelo transportador (Kg). É a soma de todo o peso do material transportado ao longo da correia, do peso equivalente das partes rotativas (motores, redutores, acoplamentos e tambores motrizes) e do peso equivalente dos equipamentos móveis do transportador (material, tambores movidos, correia e rolos).
tp = tempo de parada natural da correia (s)
V= Velocidade nominal da correia (m/s)
Exemplo:
Tensão Efetiva da Correia: 26,8 KN
Velocidade da Correia: 3,3 m/s
M: 39.280 Kg
Sendo assim:

4 – CÁLCULO DA MASSA TOTAL DO TRANSPORTADOR
A massa movida e massa total, é o somatório de todos estes pesos mostrados abaixo:
Massa Movida: Peso do Material, Peso da Correia, Peso equivalente Roletes de Carga, Peso equivalente Roletes de Retorno, Peso equivalente dos Tambores movidos.
Massa Total: Massa do Acionamento (motores, acoplamentos, redutores e tambores motrizes) + Massa Movida
Exemplo
Peso do Material
- Peso linear do Material: 252,5 Kg/m
- Comprimento carregado da correia: 63,8 m
- Peso do Material: 252,5 Kg/m x 64,6 m = 16.311,5
Peso da Correia
- Peso linear da Correia: 45,7 Kg/m
- Comprimento desenvolvido da correia: 165 m
- Peso da correia: 45,7 Kg/m X 165 m = 7.540,5 Kg
Peso equivalente Roletes de Carga
- Peso rotativo de cada rolete: 57 Kg
- Quantidade de Roletes de Carga: 65
- Peso equivalente Roletes de Carga: 57 Kg X 65 = 3.705 Kg
Peso equivalente Roletes de Retorno
- Peso rotativo de cada rolete: 50,7 Kg
- Quantidade de Roletes de Retorno: 23
- Peso equivalente Roletes de Retorno: 50,7 Kg X 65 = 1.166,1 Kg
Peso Tambores Movidos
- Tambor 1: 530Kg, Tambor 2: 530Kg, Tambor 3: 967 Kg, Tambor 4: 527Kg, Tambor 5: 530 Kg, Tambor 6: 530Kg, Tambor 7: 967Kg.
- Peso Total: 4.581 Kg.
Massa Movida: 16.311,5 Kg + 7.540,5 Kg + 3.705 Kg + 1.166,1 Kg + 1.166,1 Kg + 4.581 Kg

Massa Total: Massa Movida + Massa do Acionamento = 33.304 Kg + 6.168 Kg = 39.472 Kg
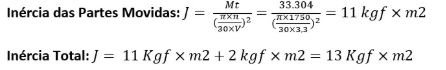
5 – DIMENSIONAMENTO DE VOLANTE DE INÉRCIA
A fim de se aumentar o tempo de parada da correia, pode-se instalar volante inércia na entrada do redutor. A função do volante de inércia é de acrescentar massa movida do transportador, aumentando assim o tempo de parada natural da correia.
Antes de se preocupar com a dimensões do Volante de Inércia, deve-se primeiro saber qual o tempo de parada necessária para a correia. No exemplo dado anteriormente, o tempo de parada do transportador foi de 4,8 s.
Supondo que seja desejado um tempo de parada de 11 s, deve-se então calcular a massa total necessária:

Onde:
tp= Tempo de parada natural (11s)
Te= Tensão Efetiva da Correia (26.800 N)
V= Velocidade da Correia (3,3 m/s)
m= Massa total do transportador (Kg)
Como a massa total do transportador já foi calculada como sendo 39.472 Kg, necessita-se de uma massa adicional de 49.861 Kg (89.333 Kg – 39.472 Kg).
Calcula-se então a inércia necessária para o nosso Volante:
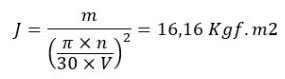
Onde:
m = Massa adicional (49.861 Kg)
n= Rotação do Motor (1750 rpm)
V= Velocidade da Correia (3,3 m/s)
J= Inércia necessária para o Volante (kgf-m2)
Define-se então o raio e a massa do Volante de Inércia através de um cálculo iterativo entre as duas variáveis, onde o Raio é limitado pelo espaço físico ou pela velocidade periférica máxima (150 m/s). Após definido o Raio, calcula-se a massa do Volante para posteriormente determinar a sua espessura.

Onde:
J = Inércia do Volante (16,16 Kgf-m2)
R = Raio do Volante (m)
r = Raio do eixo onde o volante é instalado (0,0275 m)
t= Espessura do Volante de Inércia (m)
d= Densidade do Aço (8050 kg/m3)
Portanto, considerando um Raio de 369 mm, encontra-se uma massa de 236 Kg, o que seria necessária uma espessura de 70 mm para que o volante tenha tal massa.
Uma última verificação quanto a velocidade periférica do Volante de Inércia é feita. Tal valor não deve ser maior que 150 m/s a fim de limitar o tamanho do Volante.

Onde:
V= Velocidade Periférica do Volante (m/s)
R= Raio do Volante (0,369 m)
n = Rotação do Motor (1750 rpm)